FUNDAMENTALS OF INTERFACIAL SCIENCE
This brief introduction into interfacial phenomena is thought to help users of interfacial measuring technique to better understand what instrument is most suitable for a certain problem, and which possibilities do exist to understand the measured data.
There are many motivations for interfacial studies. Many applications are based on foams or emulsions. As an example the principle features of an emulsion system are shown in the following schematic.
There are many motivations for interfacial studies. Many applications are based on foams or emulsions. As an example the principle features of an emulsion system are shown in the following schematic.

An emulsion consists of a huge number of drops of different size interacting with each other. When two drops contact each other a liquid film is formed which is stabilized by adsorbed molecules, here symbolized by adsorbed surfactants. The film is built up by two adsorption layers. Hence, the properties of these adsorption layers, also subjected to deformations like compression and expansion or shear, is of essential importance for understanding the formation and stabilisation of emulsions. The situation with foams has a lot in common with emulsions and similar problems arise.
Adsorption of surfactants
Surfactants are molecules with a so-called amphiphilic character, i.e. they consist of a hydrophilic part and a hydrophobic part. While the hydrophilic headgroup prefers to be located in water, the hydrophobic tail prefers to be in air or oil, which makes the interface an ideal location for such amphiphilic molecules.

Key parameters of adsorption layers are the dynamics of adsorption during their formation, the equilibrium parameters of adsorption, and the rheological behaviour, including the elasticity and viscosity of dilation and shear (in a broad frequency interval). At the interface between two immiscible liquid, such as water and oil, molecules adsorb and partly pass into the oil phase. The distribution of the surfactant between the two phases is given by the distribution coefficient.

Adsorption of polymers
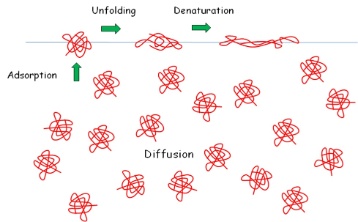
Also polymers, in particular protein, are surface active. As example the process of adsorption of a protein at the water-air interface is shown here. The protein is transported in the solution bulk by diffusion, arrives at the surface and adsorbs, and at the interface it is changing its conformation. The extent of this unfolding and denaturation process depends on the space available at the interface.
Adsorption Isotherms
The surface activity of a surfactant or protein is best documented by the so-called adsorption isotherm. This isotherm represents the relationship between the bulk concentration c and the surface excess Γ (adsorption) at the interface. The most simple relationship is the linear Henry isotherm:
The most frequently used isotherm, however, is the Langmuir isotherm, which contains two physical parameters, a characteristic concentration a at which half of the interface is covered by the surfactant, and the maximum amount that can be adsorbed Γ∞:
The following schematic shows how Γ is changing with increasing concentration c in the solution bulk.

Methods for measuring equilibrium adsorption
Ellipsometry is a possibility to measure directly the adsorption of surfactants at liquid interfaces. For pros and cons and range of applicability, please look into literature (H. Motschmann and R.Teppner, Ellipsometry, in “Novel Methods to Study Interfacial Layers”, Studies in Interface Science, Vol. 11, D. Möbius and R. Miller (Eds.), Elsevier, Amsterdam, 2001, p. 1). Easier accessible is the surface tension of a solution. Via thermodynamic models it is possible to determine the adsorbed amount from so-called surface tension – concentration isotherms g(c). The equivalent to the above Langmuir isotherm is the von Szyszkowski isotherm:
g0 is here the surface tension of the pure solvent, and R and T are the gas low constant and the absolute temperature.
The classical isotherms, for example Langmuir and also the more advances Frumkin isotherms, do not describe perfectly all experimental data. In recent time, better models have been developed, which are summarised in a book (V.B. Fainerman, D. Möbius and R. Miller (Eds.), Surfactants – Chemistry, Interfacial Properties and Application, in Studies in Interface Science, Vol. 13, Elsevier, 2001 ). As an example, the following graph shows the surface tension isotherms of five members of the homologous series of fatty acids, a classical model surfactant.

Kinetics of adsorption
The adsorption process of surface active molecules at interfaces is a time process. When a fresh interface is formed, no molecules are adsorbed. Those close to the interface can adsorb first, creating a concentration gradient in the layer adjacent to the interface. Due to diffusion molecules move and re-establish a homogeneous distribution in the solution bulk. The schematic below shows the steps of such an adsorption process.
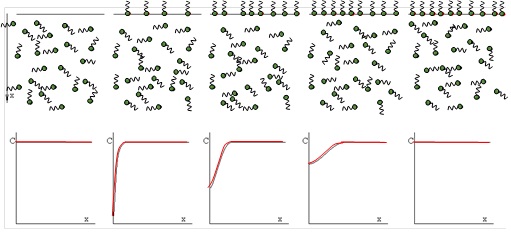
The graphs demonstrate how the concentration gradient towards the surface first increases and then decreases with time and leads finally again to a homogeneous surfactant distribution in the solution bulk. The theoretical model which describes the "diffusion controlled" adsorption process of surfactants at a solution surface was derived by Ward & Tordai in 1946 and results in a Volterra-type integral equation:

where D is the diffusion coefficient and co is the surfactant bulk concentration. The equation describes the change of Γ(t) with time t, however, its application to dynamic surface tension data g(t) is not simple. In the book mentioned above by Fainerman, Möbius and Miller a paragraphs is dedicated to the general physical idea of all adsorption kinetics models, and to particularities of various models.
Dynamic surface tension with overlapping time intervals
The adsorption dynamics is best studied by measuring the dynamic surface tension, or in case of interfaces between two immiscible liquids the dynamic interfacial tension. There are various methods available for such measurements having different time windows. Methods with complementary time windows are needed, even for the study of one surfactant, as the rate of adsorption depends on its surface activity and the concentration in the solution bulk. This is best seen from the following graph which shows the dynamic surface tension measured with a drop shape technique (see PAT-1M and PAT-2S, products of SINTERFACE).
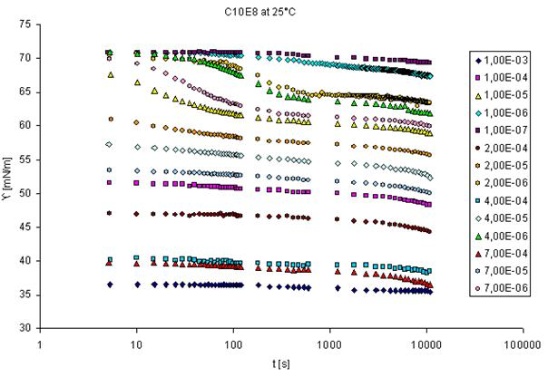
This method yields values for very long adsorption times (here up to about 10.000 s) however, for short times no data are provided by this technique. For a concentration up to 7×10-6 mol/l this time interval seems to be sufficient, for higher concentrations, however, the surface tensions at 5 seconds (the lowest time measured by the PAT-1M here, actually it can start from about 1 s), are significantly lowered due to adsorption. For such surfactant concentrations measurements at much shorter adsorption times are required. The only technique that provides data at adsorption times down to 1 ms and even less is the bubble pressure tensiometry (see BPA-1S and BPA-2S from SINTERFACE). For dynamic interfacial tensions short adsorption times like 1 ms are not accessible by any existing method. The following schematic gives an overview of existing methods for dynamic surface and interfacial tensions and the corresponding time windows. The drop pressure module (DPA-1 and ODBA-1) is the first experimental set-up which allows to measure at short adsorption times. Depending on experimental details, times even below 10 ms could be accessible.

The choice of a suitable method is sometimes not so easy, as for certain problems many methods exist, and all of them have advantages against others, in respect to easy handling, available temperature control, applicability to liquid-gas and liquid-liquid interfaces etc. What however, becomes evident as well is, that there is no method that covers the whole range of time and needs. Note, for highly concentrated solutions, i.e. for most surfactant solutions above the CMC, even 100 μs appear to be a long adsorption time. An actual summary of experimental possibilities using drop and bubble methods and an excellent selection of experimental examples has been published recently (R. Miller and L. Liggieri (Eds.), Bubble and Drop Interfaces, in “Progress in Colloid and Interface Science”, Vol. 2, Brill Publ., Leiden, 2011, ISBN 978 90 04 17495 5).
top
2D Rheology - general idea
When interfacial layers are deformed there are forces acting against this deformation. There are principally two forms of deformation:
- shear deformation: changing shape of the interface at constant area
- dilational deformation: constant shape but changing surface area.
The possibility of expansion and compression of an interfacial layer is a peculiarity different to bulk rheology, where in a first approach incompressible liquids are assumed.

Expansion or compression deformation
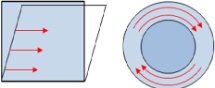
Shear deformation
Both types of deformation provide one elasticity and one viscosity parameter, each.
A first complete book on interfacial rheology was published recently (R. Miller and L. Liggieri (Eds.), Interfacial Rheology, Vol. 1, Progress in Colloid and Interface Science, Brill Publ., Leiden, 2009, p. 567-613, ISBN 978 90 04 17586 0).

A book was published recently which for the first time summarises the main ideas and available instrumentation, including also a number of well selected experimental examples (R. Miller and L. Liggieri (Eds.), Interfacial Rheology, in “Progress in Colloid and Interface Science”, Brill Publ., Vol. 1, Leiden, 2009, ISBN 978 90 04 17586 0).
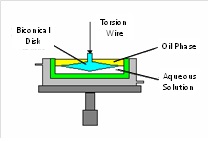
Shear rheology
In shear rheology experiments are performed such that the viscosity and elasticity of the interfacial layer is measured. Typical experiments are those using a torsion pendulum. The top view of a torsion pendulum with the shear field is shown here.


The surface shear viscosity of ß-casein is shown in the following figure. Depending on the bulk concentration, the shear viscosity increases and then drops down again.

This behaviour can be explained by the structure of the interfacial layer formed by the
β-casein molecules, which is more crosslinked at lower surface coverage with more unfolded protein molecules, and less crosslinked at higher surface coverage.
top
Dilational rheology
For the dilational rheology the parameter E0 is defined as the dilational elasticity module
This parameter results directly from the interfacial thermodynamics. Using for example the Langmuir isotherm (see above) we obtain the following relationship
When harmonic perturbations are imposed to an interfacial layer an oscillation behaviour of the interfacial tension is observed. This behaviour can be described by the complex elasticity E(iω) defined by the following equation
For a diffusion controlled exchange of matter we obtain
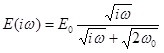
where the real and imaginary parts are given by

and
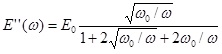
Experiments are performed to measure the frequency f dependence of E' and E" in order to find the characteristic relaxation frequencies of an interfacial layer. Here,
A typical dilational experiment can be carried out with the drop shape tensiometer PAT.
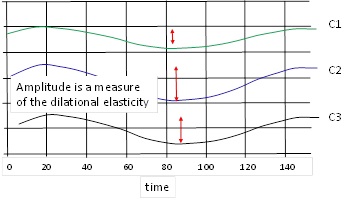
Using the dosing system the drop area can be subjected to transient or harmonic perturbations, such as those shown in the following graph: after 3 h keeping the drop surface area constant (10800 s) first 3 square pulses are performed, and then 3 oscillations each at 2 frequencies.

From such experiments we can determine the dilation elasticity and viscosity. The phase lag between g(t) and the area change is a measure of the dilational viscosity.

On the other hand, the amplitude of g(t) is a measure of the elasticity at the given frequency.
With increasing bulk concentration the elasticity E' increases and passes through a maximum. The same happens with the viscous term E", as one can see in the following graph showing results for a model surfactant (dodecyl dimethyl phosphine oxide) at a frequency of 0.3 rad/s = 0.048 Hz.
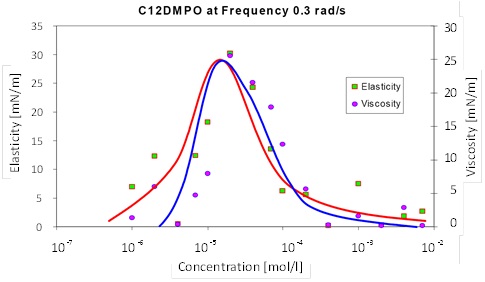
The measured dilational rheology is a function of frequency and only at very high oscillation rates a plateau value is reached, which theoretically should coincide with the value of E0 obtained from the adsorption isotherm.
top
Foams and emulsions
For the characterization of emulsions, essentially the evolution of drop size distribution with time includes all important information. Unfortunately, there is no commercial instrument that allows a general study of this behaviour. Main problem is the automation of such an analysis and the interference of sedimentation/creaming processes.
For foams the situation is quite different, as there are various commercial instruments on the market. Most of them are based on the procedure proposed by Ross and Miles, i.e. on the measurement of the breakdown of a foam column to half of its height. Some instruments also measure the drainage as function of time, however, mainly under not well defined conditions. The Foam Analyzer FA-1 produced by SINTERFACE is the first instrument that allows to determine drainage and stability of a foam under standardized conditions, i.e. as a function of applied partial vacuum. This provides the possibility of a quantitative correlation between foam and foam film properties and gives access to a deeper understanding of processes stabilizing and destabilizing foams.
The new tool DBMM, the Drop Bubble Micro Manipulator, represents a unique opportunity to mimic the situation in foams and emulsions. Two bubbles or drops can be formed at the tip of a capillary, each, and then manipulated against each other, as it is the case in real liquid disperse systems. Even the asymmetric case of a bubble and a drop can be created (see also R. Miller and L. Liggieri (Eds.), Bubble and Drop Interfaces, in “Progress in Colloid and Interface Science”, Vol. 2, Brill Publ., Leiden, 2011, ISBN 978 90 04 17495 5).
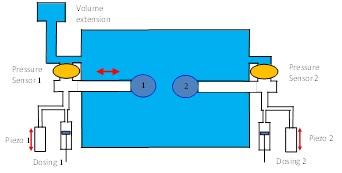
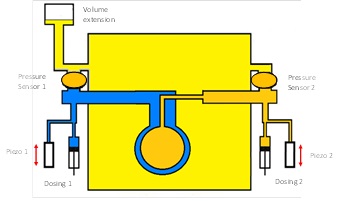
The same tool with small modifications can be also used to study elementary processes in multiple emulsions, where for example water drops are dispersed in a oil matrix, while inside these water drops oil droplets are dispersed. This type is called oil-in-water-in oil double emulsion (o/w/o).

The DBMM would then be equipped with a special double capillary in order to provide the situation of a drop formed inside a drop which in turn is immersed into another liquid, which could be the same oil like the internal dispersed phase.
top


